CBOW and Skip-gram
Explanation
We have a vocabulary of size $V$. Each word $x$ is represented as a one-hot vector.
We want to convert the word to a latent space of dimension $N$. This is achieved by using a matrix $\mathbf{W} \in \mathbb{R}^{V \times N}$ [slim] where each row $i$ corresponds to the latent vector for word $i$. (Notice the inherent network structure.)
We also want to transform the latent vector back to the original space. The is achieved by using a matrix $\mathbf{W}’ \in \mathbb{R}^{N \times V}$ [fat] where each column $j$ is responsible for the score calculation for word $j$. The result vector contains scores for every word in the vocabulary.
The basic model works as: $$ \boxed{\mathbf{x}} \overset{\mathbf{W}}{\longrightarrow} \boxed{\mathbf{h} = \mathbf{x}^T\mathbf{W} = \mathbf{v}_{w_I}} \overset{\mathbf{W}'}{\longrightarrow} \boxed{u_{j} = (\mathbf{v}'_{w_j})^T \cdot \mathbf{h}} $$ $\mathbf{v}_{w_I}$ is the row vector of $\mathbf{W}$ for word $wI$ and $\mathbf{v}{w}$ is called input vector.
$\mathbf{v}'_{w_j}$ is the $j^{th}$ column vector of $\mathbf{W}'$ and $\mathbf{v}'_{w}$ is called output vector.
We can obtain the posterior distribution of words by using softmax: $$ \begin{aligned} P[w_j | w_I] = \frac{e^{u_j}}{\sum_{i=1}^{V} e^{u_i}} = \frac{e^{(\mathbf{v}'_{w_j})^T \cdot \mathbf{v}_{w_I}}}{\sum_{i=1}^{V} e^{(\mathbf{v}'_{w_i})^T \cdot \mathbf{v}_{w_I}}} \end{aligned} $$
CBOW model works by using context words as input and center word as label.
Skip-gram model works by using center word as input and context words as labels.
For training, the skip-gram model multiplies the scores of the context words. $$ \begin{aligned} \min J &= -\log P[w_{c-m}, \dots, w_{c-1}, w_{c+1}, \dots, w_{c+m} | w_{c}] \\ &= -\log \prod_{j=1, j \neq m}^{2m} P[w_{c-m+j} | w_{c}] \end{aligned} $$ The CBOW model calculates the cross-entropy loss of the output vector with the center word. $$ \begin{aligned} \min J &= -\log P[w_{c} | w_{c-m}, \dots, w_{c-1}, w_{c+1}, \dots, w_{c+m}] \\ &= -\log P[u_c | \hat{\mathbf{v}}] \\ \hat{\mathbf{v}} &= \frac{\mathbf{v}_{c-m} + \cdots + \mathbf{v}_{c+m}}{2m} \end{aligned} $$
Demonstration
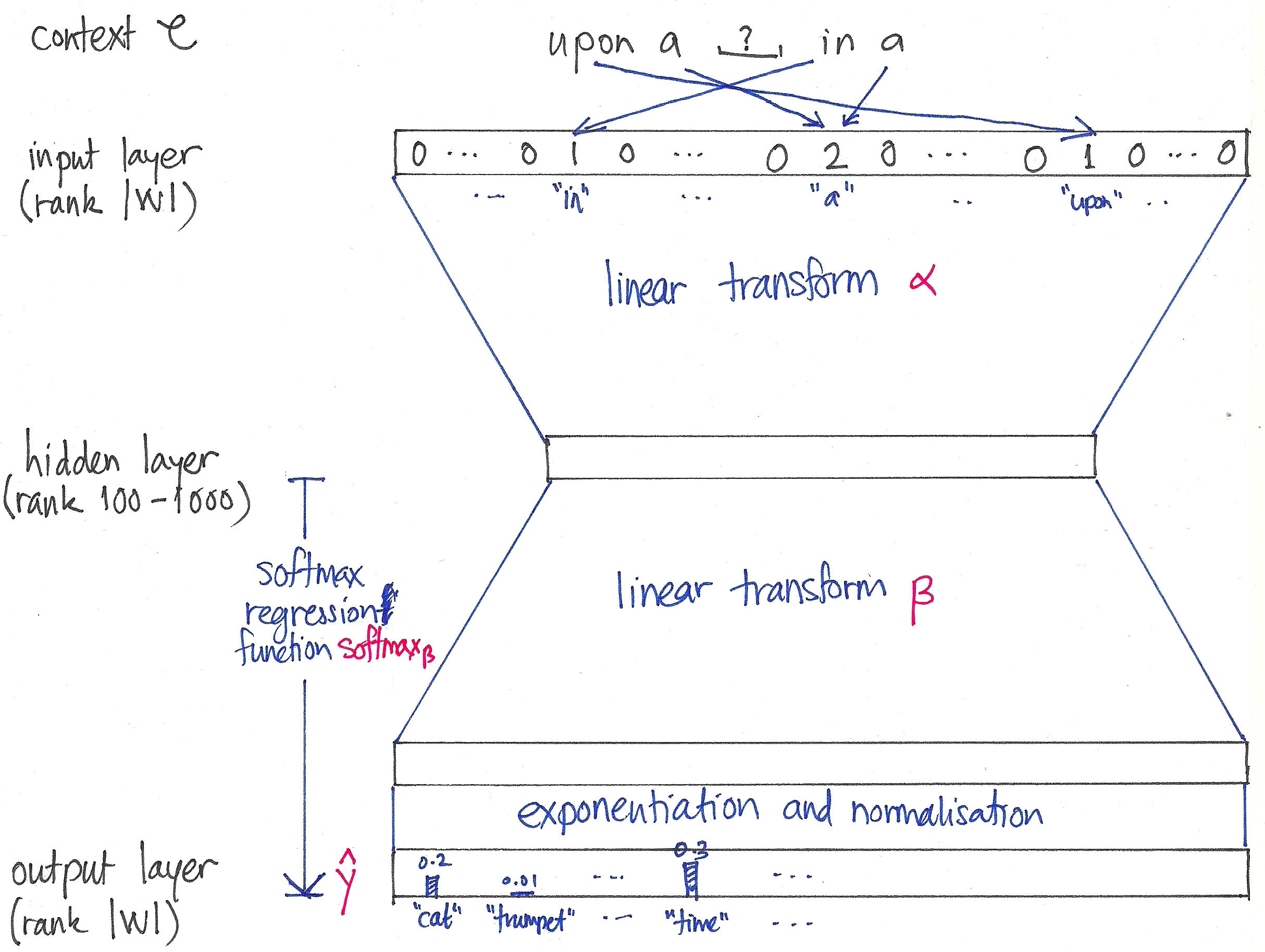
Data Format:
